由题意知△ABC为等腰直角三角形,设AC=BC=a。据旋转对称性及∠ECF=45°,可得CE=CF且EF∥AB。利用相似三角形性质与勾股定理可推得EF=$frac{a}{sqrt{2}}$。
-
-
如图,在△ABC中,∠ACB=90°,D、E是AB边上的两个点,且AD=AC,BE=BC
(1 若∠A=60°,求∠DCE的度数
(2)若∠A=50°,求∠DCE的度数
(3)若∠A=a°,求∠DCE的度数
(4)试根据解题结果归纳出一个一般性的结论
....是不是这个题目。。
提示:若∠A=60°,求∠DCE=45°;若∠A=50°,求∠DCE=45°
若∠A=a°;那么
1、在△ABC中,∠ACB=90°,若∠A=a°,则∠B=90°-a°;
结论
△ADC中,AD=AC,则∠ACD=90°-a°/2;
△BCE中,BE=BC,则∠BCE=45°-a°/2;
∠ACE=90°-∠BCE=90°-(45°-a°/2)=45°+∠a°/2;
∠DCE=∠ACD-∠ACE=(90°-a°/2)-(90°+∠a°/2)=45° -
∵在rt△abc中角acb=90°,
在△acd中,ad=ac,则∠acd=∠adc.
在△bce中,bc=be,则∠bce=∠bec,
则∠ace=∠bcd,∠ceb=∠adc=∠ecb,
∠cab=∠cba=45度,
而,∠cdb=∠cab+∠acd=45+∠ace+∠ecd,
∠cdb+∠dcb+∠cbd=180,
(45+∠ace+∠ecd)+∠dcb+∠cbd=180,∠ace=∠bcd.
2∠ace+∠ecd=90度,......(1)式,
∠cad+∠acd+∠adc=45+2(∠ace+∠ecd)=180,
即,(∠ace+∠ecd)=135/2.......(2)式.
由(1),(2)得,
∠ace=45/2,∠ace=∠bcd,
2∠ace+∠ecd=90度,
∠ecd=90-45=45度 -
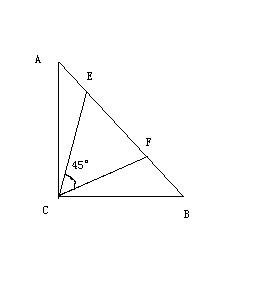
(1)证明:如图,∵∠ACB=90°,AC=BC
∴△ABC是等腰直角三角形.
所以∠A=∠B=45°=∠ECF.
∠CEF=∠ACE+∠A=∠ACE+45°
∠ACF=∠ACE+∠ECF=∠ACE+45°
∴∠ACF=∠CEF
又∵∠A=∠B
∴△ACF∽△BEC.
(2)证明:由上题结论△ACF∽△BEC可得
AC:BE=AF:BC
∴AC×BC=AF×BE
又∵S=1/2AC×BC
∴AC×BC=2S
∴AF×BE=2S.
(做这种题要注意根据题目所给的条件找出对应边与对应角)
-
应该是过E作AC的垂线交CD的延长线于点F吧!怎么会有两个E呢 证明如下 ∵EF⊥AC ∴∠AEF=90° 又∵∠ACB=90° ∴EF‖CB ∴∠DCB=∠F ∵CD⊥AB ∴∠DCB+∠B=90° 又∵∠ACB=90° ∴∠A+∠B=90° ∴∠DCB=∠A ∵∠DCB=∠F ∠DCB=∠A ∴∠F=∠A 在△ACB与△FEC中 ∠A=∠F ∠ACB=∠FEC CB=CE ∴△ACB≌△FEC(AAS) ∴AB=FC
