已知如图在rt三角形abc中角acb等于90度,∠BAC=60°,BC的垂直平分线分别交BC和AB于点D，E，点F在DE的延长线-PChome电脑之家

智能回答

已知如图在rt三角形abc中角acb等于90度,∠BAC=60°,BC的垂直平分线分别交BC和AB于点D，E，点F在DE的延长线

展开

没找到满意答案？去问豆包AI智能助手

取消复制问题

huihuoxiao

由题意，Rt△ABC中，∠ACB=90°，∠BAC=60°，则∠ABC=30°。BC的垂直平分线DE交BC于D，AB于E，则EB=EC。延长DE至F，因对称性，可得EF=ED，故F与C关于DE对称，△ECF为等边三角形。
XINXINKS

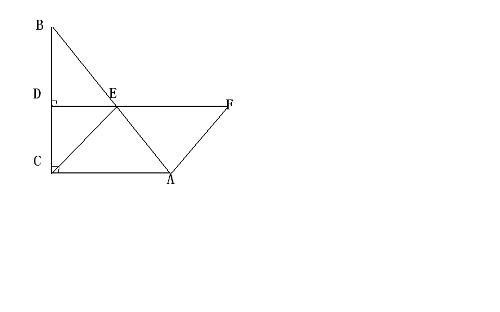解：在Rt△BDE中，
∠B＝30°，
∴∠BED＝60°，
∵DE为BC中垂线，
∴∠CED＝∠BED＝60°，
∴∠AEC＝180－2×60＝60°，
∵∠BAC＝60°，
∴△ACE为正△，
∴AF＝CE＝AE，
∵∠AEF＝∠BED＝60°，
∴△AEF为正△，
∴∠F＝∠ACE＝60°，∠CEF＝∠CAF＝120°，
∴四边形ACEF为平行四边形，
在△ACE中，
AC＝CE，
∴平行四边形ACEF为菱形。
13865018362

(1) ∵AC＝CB 又∵∠ACE＝∠CBD＝90° 又∵∠EAC＝∠DCB＝90°－∠ACF ∴△ACE≌△CBD ∴AE＝CD (2) ∵BD＝5cm ∴CE＝5cm ∴CB＝10cm ∴AC＝10cm
toplink

（解：在Rt△BDE中，
∠B＝30°，
∴∠BED＝60°，
∵DE为BC中垂线，
∴∠CED＝∠BED＝60°，
∴∠AEC＝180－2×60＝60°，
∵∠BAC＝60°，
∴△ACE为正△，
∴AF＝CE＝AE，
∵∠AEF＝∠BED＝60°，
∴△AEF为正△，）→虽然前面解的也不好但我还是得尊重下你但是后面也太烂了把
接下来我改的∴AE=AF=EF

∵等边△AEC

∴CA=CE=AE

即CA=CE=AE=EF

∴四边形ACEF为菱形。→好好学数学把，没学好就出来学人家混！
linxusheng456

证明：∵∠ACE=90°，DE垂直平分BC， ∴DF∥AC，AE=CE， ∴∠B=∠BCE， ∵∠B+∠BAC=90°，∠ACE+∠BCE=90°， ∴∠BAC=∠ACE， ∴AE=CE=AE， ∵∠BAC=60°， ∴ΔACE是等边三角形， ∴∠AEF=∠CAE=60°， ∵AF=CE=AE， ∴ΔAEF是等边三角形， ∴EF=AE=AF=AC=CE， ∴四边形ACEF是菱形。************************************************************************************ ^__^真心祝你学习进步，如果你对这个答案有什么疑问，请追问，另外如果你觉得我的回答对你有所帮助，请千万别忘记采纳哟！如果有其他问题，欢迎向我求助。与本题无关的就请不要追问了。答题不易呀。懂了记得选满意。 ************************************************************************************
Simonxiaoting

证明：延长CE和BA交于F

∵BE平分∠ABC

∴∠CBE=∠FBE

∵BE=BE

BE⊥CF

∴△CBE全等于△FBE

∴CE=FE=CF/2

∵∠BAC=90°

∠BDA=∠CDE

∴∠ABD=∠ACE

∵AB=AC

∠BAC=∠CAF=90°

∴△BAD全等于△CAF

∴BD=CF

∴CE=BD/2

已知如图在rt三角形abc中角acb等于90度,∠BAC=60°,BC的垂直平分线分别交BC和AB于点D，E，点F在DE的延长线

最新回答更多>

相关问答

举报

举报成功

已知如图在rt三角形abc中角acb等于90度,∠BAC=60°,BC的垂直平分线分别交BC和AB于点D，E，点F在DE的延长线

最新回答 更多>

相关问答

举报

举报成功

最新回答更多>